Time
Mark Pottenger
Keeping Time
Mankind has probably measured time almost since the beginning of conscious awareness. Anything we might say about timekeeping in prehistory is guesswork, but we also have a few millennia of the history of timekeeping. The most obvious observable indications of the passage of time are the day/night cycle, the annual cycle of seasons, and the motions of the Moon, stars, and wanderers (planets, comets, etc.). For most of history, precise times were not needed or wanted. Day/night, then sunrise/noon/sunset, then canonical hours (matins, lauds, vespers, prime, terce, sext, none, compline) or Muslim prayer calls are a progression in detail. Times to that degree of detail have been measured with water dripping from a hole, a candle burning measured lengths, sand falling through an hourglass, the shadow of a stick (a sundial), mechanical clocks based on the pendulum or gears or springs, and many other ingenious inventions over many years. Modern (recent centuries) industry and modern science have led to our day of 24 hours, each hour made of 60 minutes, each minute made of 60 seconds, each second capable of being measured to an accuracy of better than one part in 1,000,000,000,000,000 by the latest atomic fountain clocks. Modern timekeepers use occasional leap seconds to reconcile the extremely consistent international time standards from atomic clocks to the more variable motions of the Earth.
Count Zero
A sidelight related to time is date. The year 2000 will be the last year of the second millennium C.E. (common era, the non-religious version of A.D.). The year 2001 will be the first year of the third millennium C.E. C.E. dates started with the year 1, so the millennia are 1-1000, 1001-2000, 2001-3000, 3001-4000, etc. At the time and place the C.E. calendar came into use, Roman numerals were the standard notation for numbers. Roman numerals have no zero, so the calendar goes from 1 B.C. to 1 A.D.
Time and Longitude
Any history of time and timekeeping is inevitably intertwined with the history of travel, longitude and communications. When people traveled slowly or only for short distances, time based on simple visual observations at any location was adequate for all practical use. When people started to regularly travel faster and communicate over longer distances, the differences between the observable times at different locations (longitudes) started to become an issue (360 degrees of longitude = 24 hours of time, 15 degrees = 1 hour, 1 degree of longitude = 4 minutes of time). Two travel developments are especially important here: ships and railroads.
A few centuries ago, the “problem of longitude” was a major scientific/technological issue. Navigation at sea was subject to severe limits and required special caution because there was no way for people on a ship to determine their longitude from observation. An error could make the difference between safety and shipwreck. Many prominent astronomers and other scientists (including Isaac Newton) worked on the problem, but it was finally solved more by technology and mathematics than by science. (One of the reasons a lot of people tackled the problem was that England, after losing many ships, offered a large monetary prize for a solution.) In the mid-1700s, John Harrison developed chronometers that could keep time reliably enough that a ship could use them to determine its longitude. In essence, time at an observer’s location can be determined by careful observation of the sun, moon and stars, followed by some calculations. With an accurate chronometer set to the time of a known location, determining longitude became a matter of getting the difference between the time kept by the chronometer and the time determined from observations and calculations. Once the observed (ship) time and the chronometer (port) time are in the same framework (both apparent or both mean), the difference gives longitude east or west of the original location directly. Note: mechanical chronometers measure time in even intervals, unlike the more variable cycles in the sky.
Time balls (large balls dropped to mark times) are relics of the era when ships depended on accurate chronometers. An English sea captain developed the system in the early 1800s and pushed until it was used in several areas. The original time balls were controlled from an observatory or other location on land where accurate observations were made to determine the local time. A large ball visible from the sea or harbor would be released so that its motion would be visible at exactly the same local time every day (mostly 1 P.M. or noon). Sailors could watch for the signal and check their chronometers. The most important information they would get was not the exact time (that was secondary) but exactly how fast or slow their chronometer was running. This let them include any needed fudge factor to account for real world mechanisms in their calculations of longitude based on that chronometer. Away from coasts and later in the century, signaling a time for people to set their clocks and watches to became the primary use of time balls.
Railroads pushed for the standardization of times in much the same way travel by ship pushed for accurate measurement of time. Railroads require accurate and careful scheduling (two trains competing for one track = trouble). Local time changes by 4 minutes for every degree of longitude you travel east or west. To be able to schedule, railroads and anyone using them had to pick a system of time everyone on a route could share. The simplest standard is to agree that all points in a given area will use the time of one point in the area. For England’s railroads in the 1800s, the time at Greenwich Observatory, already important from nautical use, became the standard. Starting 31 July 1848 (per Holyhead web site) and continued until 1939, the Irish Mail train carried from London to Ireland a watch (pocket chronometer) set to GMT at the Greenwich Observatory. Arrivals, departures and station clocks all along the route were all set or corrected every day based on that watch.
Railroads were a driving force for time standards well beyond England. Similar developments occurred in the United States in the mid-1800s, only on a larger scale. The U.S.A. covers so many degrees of longitude that it is several hours of time from coast to coast, so multiple standard times developed instead of just one. There were 50 to 100 (depending on who you read) railroad time standards in the U.S.A. before time zones were established in 1883. The first U.S. time zones were established by the General Time Convention of October 11, 1883 (a meeting of railroad superintendents). U.S.A. zone-based time standards were transmitted by telegraph starting at 12 Noon on Sunday, November 18, 1883. The time zones were a de facto creation of the railroads, which everyone else in the country eventually followed, but there was no federal law governing time zones until the Act of March 19, 1918.
Time zones for the rest of the world outside the U.S.A. were established by the International Meridian Conference held in Washington, DC in October 1884. This conference established Greenwich Observatory as the zero point for measuring longitudes on the Earth and established time zones. The final act of the Conference was dated 22 October 1884, and several sources mention 1 November 1884 as the start of world time zones.
Communications technologies (telegraph, telephone, radio, television, satellites) have increased the need for and the ability to synchronize common schedules or times. Time signals from Greenwich Observatory were sent by telegraph starting in 1852. All the advances in communications technologies since then have made it easier to talk or broadcast across many degrees of longitude (and hours of local time). (On the navigation side, the GPS network, combined with a special receiver with some computing power, now makes a determination of longitude a simple pushbutton operation, replacing many hours of manual observations and calculations.)
Saving Daylight
Once zone-based times became the standard around the world, a new form of tinkering began. Daylight saving time was first used in World War I and has been a source of chaos in birth records ever since. The premise behind daylight saving time (also called summer time in some areas) is quite simple: it saves power. Enough of the activity in industrial societies is on an 8-5 or 9-5 schedule that changing the clocks shifts an hour of daytime (awake) activity from darkness to daylight. Shifting this much activity cuts the use of electric lights and possibly some other power consumption enough to create a measurable energy savings, so it should really be called Power Saving Time or Energy Saving Time. This was the primary argument that got daylight saving time used during the World Wars and during certain other power shortages. There have also been arguments that the shift in activity reduces some kinds of accidents and might reduce crime.
The use of daylight saving time has been subject to extremely chaotic degrees of local control, so it is a source of major headaches in astrological data. In the U.S.A. between World War I and World War II and from the end of World War II until the passing of the Uniform Time Act of 1966, individual cities, counties and states controlled the use of daylight saving time. There were parts of the country where you could go through multiple time changes in a few miles. The boundaries of time zones were also moved quite a bit during those periods. One of the bits of time change research at ACS years ago involved reading old Interstate Commerce Commission records for clues to zone changes. The starting and ending dates of daylight saving time also varied a lot. The Uniform Time Act finally reduced the chaos by establishing nationwide rules for the start and end of daylight saving time (last Sunday in April to last Sunday in October). A state could vote to not use daylight saving time, but no smaller entity could be exempt. The Act was amended in 1972 to allow states with more than one time zone to exempt the part of the state in one zone from daylight saving time. The act was amended in 1986 to move the start of daylight saving time to the first Sunday in April starting in 1987. The situation in the rest of the world is at least as confusing as the U.S.A. before the Uniform Time Act. Most of Europe just agreed on standard daylight saving time change dates a few years ago. Two large atlases from ACS and a number of other books and articles around the world are devoted to attempts to accurately track the history of the use of daylight saving time.
Time in Astrological Calculations
There is a mathematical error circulating in parts of the astrological community: use of the equation of time in calculating modern charts. (Failure to use the equation of time in ancient charts is also common.) I have previously written articles related to this topic for the Sagittarius 1986 and Sagittarius 1996 issues of The Mutable Dilemma. I hope the material here is clear enough to show when it is appropriate to use the equation of time.
A day, which we divide into 24 hours, is a unit of time based on the rotation of the Earth. A key question for any work with time is: rotation with respect to what? If you measure Earth’s rotation with respect to fixed stars or the zero Aries point, you are dealing with sidereal time. If you measure with respect to the Sun, you are dealing with solar time. Since the Earth moves about a degree in its orbit around the Sun during one sidereal day, it takes about 4 minutes longer to finish a rotation with respect to the Sun and complete a solar day. Even though the sidereal and solar days are of different lengths, each is divided into 24 hours of 60 minutes of 60 seconds, so we must label very clearly when we work with times in astrology. Also, since the Earth’s orbit around the Sun is elliptical rather than circular, the length of a day from apparent noon to apparent noon changes through the year. We cope with this variability by using a mean (average) day for most purposes.
Time based directly on the Sun's apparent position due to the Earth’s various uneven motions, which varies up to 16+ minutes from a mean by the effects of the equation of time, was used until the late 1700s or early 1800s, with the changeover date varying from country to country. This system of time was called sundial time or Local Apparent Time, and is available in the CCRS Horoscope Program with the time type abbreviation of LAT. LAT was replaced by Local Mean Time, which deliberately eliminates the equation of time from clock time by using a mean for each meridian of longitude. This system of time is available in CCRS with the abbreviation LMT. (Note: “equation of time” is sometimes used to mean a conversion from LAT to LMT and sometimes used to mean a conversion from LMT to LAT. Be careful about whether you need to add or subtract any time you work with the equation of time.) In 1883-1884, LMT was supplemented and largely replaced by zone-based standard times. (Actually, worldwide zone definitions were agreed on in 1883-1884, but like all historical time changes the real transition was a messy patchwork that started years before the official definitions and took several more years.) Each 15-degree (1 hour) wide zone uses the LMT of the zone meridian at (approximately) the center of the zone as the standard time for the whole zone. Greenwich Mean Time (GMT) or Universal Time (UT) is the LMT and standard time of the world’s prime meridian of 0 longitude running through Greenwich Observatory in England. All clocks in normal use for the last century have kept zone-based time. Birth and event times for the last century have usually been recorded in zone-based time.
Note that all mechanical, electrical and electronic timekeeping systems—chronometers, quartz crystal clocks & watches, atomic clocks, etc.—keep time uniformly. The more accurate the system, the more uniform the time it measures. This made a switch from apparent time based on celestial variations to mean time inevitable as more and more accurate mechanical timekeeping became the norm. Modern technology could now produce a watch or clock giving apparent time by programming in the equation of time, but such a timepiece would be an oddity of little practical use. An apparent time clock would only match normal clocks a few times per year. It would be a curiosity like the lunar phase clock I bought some years ago.
Astrological ephemerides (except a few special-purpose local products) give planetary positions for times given in UT or Ephemeris Time (ET). Ephemeris Time (ET) and Terrestrial Dynamical Time (TDT) and Barycentric Dynamical Time (TDB) and Terrestrial Time (TT) are all UT +/- a delta t correction which is under 1 minute for the 20th century—the differences between these kinds of time are very small and beyond the scope of this article. (I prefer the term Ephemeris Time to the more recent terms because it makes very clear how that kind of time is used.) Calculations of planetary positions therefore require time in UT. For any zone-based time, UT is obtained by adding or subtracting the zone meridian hours and any correction for daylight or war time. Introducing equation of time effects at this point would produce the wrong UT. Angle and house calculations require a Local Sidereal Time (LST). The most direct way to get this is to get the Greenwich Sidereal Time (GST) based on the UT obtained for planetary calculations, then make a single longitude as time correction to get from GST to LST. Introducing equation of time effects (which are strictly solar time, not sidereal time) at this point would produce the wrong LST. Since UT (or ET) and LST are the only two times required to calculate a chart, the assertion that the equation of time should be used in calculating charts is patently wrong for any chart based on the normal clock times used for over a century. Only if you are getting a time directly from a sundial or other direct observations instead of from a clock would use of the equation of time be needed.
GST is defined in terms of UT (mean time, not apparent time). (Actually, UT [solar time] is astronomically derived from GST [sidereal time].) All LSTs differ from GST strictly by longitude as time. Here are a few defining quotes from the 1992 Explanatory Supplement to the Astronomical Almanac (a book describing the basis of several national ephemerides used by the astronomical community): "… UT may for most purposes be regarded as mean solar time on the Greenwich meridian" p.5 "The difference between mean solar time and apparent solar time is called the equation of time." p.74 "During the late eighteenth and early nineteenth centuries, as clocks were improved and came into extensive use at sea, apparent time was gradually superseded in civil use by mean solar time." p.75
Regarding when people switched from LAT to LMT, here is a quote from p. 4 of the 1961 Explanatory Supplement: “The NAUTICAL ALMANAC and ASTRONOMICAL EPHEMERIS for the Year 1834, …. The most fundamental change was to replace apparent time by mean time as the argument of the ephemerides. … has already been introduced with good effect into the national Ephemerides of Coimbra and Berlin….” According to Arthur Blackwell (personal communication many years ago), Geneva switched from LAT to LMT in 1780, London switched in 1792, and Paris switched in 1816. According to “Time Changes in Great Britain” by David Fisher, GMT was used for 95% of public clocks in Britain by 1855, even though GMT did not become the official legal time for all of Britain until 1 January 1880. In the few entries I spotted in Régimes Horaires pour le Monde Entier by Henri LeCorre that explicitly mention solar time, Norway is listed as changing from sundial time to mean time in 1834, Sweden is listed as changing in 1841, and Switzerland is listed as changing in 1851.
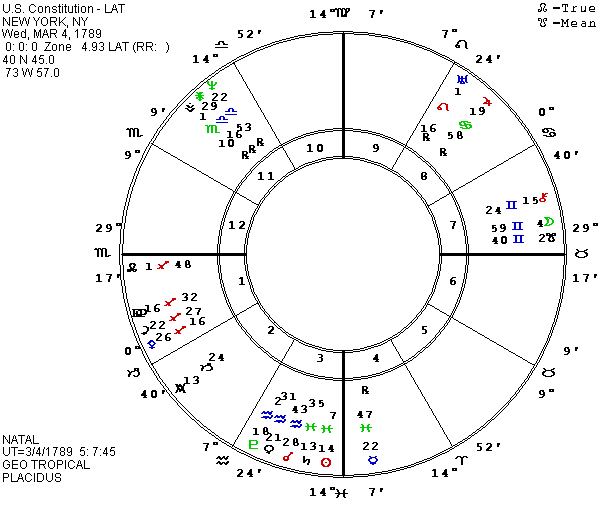
Study the two charts at the end of this article that were calculated for when the U.S. Constitution went into effect (per Campion). One was run for midnight LAT and one LMT. The LAT chart correctly has the Sun on the IC. The LMT chart only has the Sun near the IC. Notice that the UTs of the two charts differ. The equation of time is used in getting from LAT to UT but not from LMT to UT (all Solar times). After getting the UT, the equation of time is not used again! If you perform an equation of time modification to sidereal time, you will mess up the LAT chart and move the Sun away from the IC.
Sidereal Time is subject to minor corrections from obliquity and nutation, but not the equation of time (which is used only with solar time). The angle between the plane of the ecliptic and the plane of the equator is called the obliquity of the ecliptic. Nutation is a term for short period changes in the position of the Earth’s pole. Nutation corrections can be applied to the angle of the obliquity and to celestial longitude or right ascension. Nutation in right ascension, also called the equation of the equinoxes, is the difference between mean and apparent sidereal time. The equation of the equinoxes is mostly less than one second of time, with a range from about –1.16 to +1.16 seconds in the 20th century. The average size of the correction in the 20th century is about 0.7 seconds. This is a much smaller correction that the up to 16+ minutes of time of the equation of time used with solar times. The correction is so small and hard to detect in final answers that I had to look at the source code in my CCRS Horoscope Program to be able to say whether or not the program uses it (it does). Many people and programs don’t even bother with the equation of the equinoxes, working entirely with mean Sidereal Time. When the equation of the equinoxes is used to get apparent Sidereal Time, the difference is quite small. I wouldn’t worry about whether a program uses apparent Sidereal Time except for very precise work such as calculating longitudes for high harmonic numbers for a chart with extremely precise data like a rocket launch.
To give some idea of the relative importance of the equation of the equinoxes in the overall scheme of astrological calculations, consider that rounding errors in birth time and birth longitude will usually be larger. Without even getting into the question of whether a recorded time of birth is the correct time, any time recorded to the nearest minute actually means the time is as stated within plus or minus 30 seconds of time. This means that the uncertainty in a time of birth recorded with the highest precision normally used is 30 times greater than the size of the equation of the equinoxes correction of around 1 second of time. For anyone born in any city more than a mile across, unless you know the coordinates of the specific hospital you were born in, the longitude you use for your place of birth can be several minutes off. Since an error of even one minute in longitude will create an error of 4 seconds in your Sidereal Time (during the longitude as time correction step), this is again greater than the effect of the equation of the equinoxes. (I looked up my hospital of birth on a topographic map years ago, then when the ACS PC Atlas added coordinates of a lot of hospitals I checked that longitude. The two versions of my longitude of birth differ by 8 seconds of longitude (which translates to just over one-half second of time), so my uncertainty of place is smaller than the equation of the equinoxes, but most people won’t go to as much trouble.)
Both solar times and sidereal times use the terms mean time and apparent time, but we need to keep very clear that those similar terms are being applied to very different things. The difference between mean and apparent solar times is called the equation of time, and gets larger than 16 minutes of time. The difference between mean and apparent sidereal times is called the equation of the equinoxes, and is always close to 1 second of time (mostly less than a full second). LAT and LMT are quite distinct types of time. LAST (Local Apparent Sidereal Time) and LMST (Local Mean Sidereal Time) are so close to each other that the distinct abbreviations are rarely used—LST (Local Sidereal Time), which doesn’t distinguish between mean and apparent, is the most used abbreviation.
Calculation Steps and Examples
Note: everywhere below that I show +/- (add or subtract) longitude as time, add if going from west to east (e.g., U.S.A. to Greenwich, England) and subtract if going from east to west (e.g., Greenwich, England to U.S.A.). If you have a longitude expressed in degrees, minutes and seconds and need hours, minutes and seconds, divide degrees by 15 to get hours or multiply degrees by 4 to get minutes, multiply longitude minutes by 4 to get time minutes, and divide longitude seconds by 15 to get time seconds.
Here are steps to calculate times for charts:
Original time recorded in LAT (most before 1780, patchwork to 1840s):
LAT
+Equation of Time
=LMT
+/- longitude as time
=UT
(see below for more)
Original time recorded in LMT (patchwork 1780 to 1840s, most to 1883, patchwork after):
LMT
+/- longitude as time
=UT
(see below for more)
Original time recorded in Zone Time (patchwork to early 1900s):
Zone Time
If daylight/war time, subtract 1 hour (2 hours for double summer time)
+/- zone meridian longitude as time
=UT
(see below for more)
Once you have the UT (from any of the 3 starting points above):
UT (can use to look up planets in a UT ephemeris that already corrected for delta t)
+delta t (look up in table)
=ET (use to look up planets in ephemeris)
For house cusps and angles, we need to get from UT, which is a solar time, to local sidereal time. The first step is to look up the Greenwich Sidereal Time in the ephemeris for the Greenwich date of birth. Next, since 24 hours of solar time is more than 24 hours of sidereal time, determine how much the two systems will differ between the time in the ephemeris and the moment being calculated (the Solar-Sidereal Correction). The ratio is 9.856 seconds per hour. Adding GST in the ephemeris, solar time since the ephemeris moment and the SSC will produce the GST for the specified UT. Once we have the GST of the moment, we add or subtract longitude as time to get LST, which we use to look up cusps in the table of houses.
Using my own birth data as an example:
Mark Pottenger
Tucson, AZ 32 N 15’ 9” 110 W 52’ 36”
3:23 A.M. MST (Mountain Standard Time)
MST is a time zone 7 hours west of Greenwich, so add the zone time to get UT:
UT = 3:23 + 7:00 = 10:23
To express the same moment in LMT instead of zone time, adjust for longitude:
MST meridian is 105 W 0’ 0”
Local place is 110 W 52’ 36”
Difference is 5 degrees 52’ 36”
Convert 360-degree longitude to 24-hour time (1 degree longitude = 4 minutes time):
5 x 4 = 20m
52 x 4 = 208s = 3m 28s
36 / 15 = 2.4s
5 degrees 52’ 36” = 20m + 3m 28s + 2.4s = 23m 30s (truncating fraction of second)
Since the place is west of the zone meridian, subtract from zone time to get LMT:
LMT = 3:23:00 – 0:23:30 = 2:59:30
Be very clear: this is not a different time of birth than 3:23 A.M. MST—this is the same time of birth described differently.
To get from LMT to UT, add/subtract longitude of place as time:
Local place is 110 W 52’ 36” = 7:23:30
UT = 2:59:30 + 7:23:30 = 10:23
Note that unless a math error crept in UT from zone time and UT from LMT will be the same answer.
To express the same moment in LAT instead of LMT, adjust for equation of time:
Equation of time: -00:14:18 (looked up)
LAT = 2:59:30 – 0:14:18 = 2:45:12
Be very clear: this is not a different time of birth than 3:23 A.M. MST or 2:59:30 LMT—this is the same time of birth described differently.
To get from LAT to UT, add/subtract equation of time and longitude of place as time:
UT = 2:45:12 + 0:14:18 + 7:23:30 = 10:23
Note that unless a math error crept in this UT will be the same answer as before.
If you start with LAT and add/subtract the longitude of the place as time without doing anything about the equation of time, you get Apparent Time in Greenwich:
GAT = 2:45:12 + 7:23:30 = 10:08:42
I don’t know of any system of calculations that needs or uses GAT. I am simply including it here to show a complete set of possible transformations.
For planets and asteroids, look up the difference between UT and ET:
Delta t: 31s (lookup)
ET = 10:23:00 + 0:0:31 = 10:23:31
Get from UT (solar time) to sidereal time:
9 Feb 1955 GST at 0 hr UT = 9h13m15s (look up in ephemeris)
Solar-Sidereal Correction: 10:23 = 10.3833 hr x 9.856 sec/hr =102.34 sec = 1 min 42 sec
GST = 9:13:15 + 10:23:00 + 0:01:42 = 19:37:57
Once we know the Sidereal Time in Greenwich, we just need to correct for longitude to get the Local Sidereal Time of birth (the longitude as time correction is the same as above):
LST = 19:37:57 - 7:23:30 = 12:14:27
LST and latitude of birth are the two numbers we need to look up all the house cusps in a table of houses (or for a computer to calculate them).
After all those calculations, my moment of birth can be described as
3:23 (A.M.) MST
2:59:30 LMT
2:45:12 LAT
10:08:42 GAT
10:23 UT
10:23:31 ET
19:37:57 GST
12:14:27 LST
All of these labels are just descriptions of the same moment in different frameworks or from different perspectives. None of the calculations or lookups have produced a different time. All of these times can be transformed into each other within the limits of rounding errors. If any step in chart calculations produces a different time—one that can’t be transformed back to the original—that step is in error.
All of the calculations above illustrate how much easier it is these days than in the past for an astrologer to produce a chart. A few centuries ago, you had to start from LAT. The switch from LAT to LMT eliminated the need for the equation of time correction. The switch from LMT to zone times standardized the longitude as time correction in solar time on a few even-hour numbers. Time change chaos then added a new reference book step, but now a computer with the ACS PC Atlas can do that lookup automatically. Modern astrologers should understand the background of the times in charts, but as long as the programs used are reasonably bug-free they don’t have to actually deal with anything more than the recorded time of birth.
References
The Book of World Horoscopes Nicholas Campion, Cinnabar Books, Bristol, England, 1995.
Explanatory Supplement to the Astronomical Almanac Edited by P. Kenneth Seidelmann, University Science Books, Mill Valley, CA, 1992.
Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac Prepared jointly by the Nautical Almanac Offices of the United Kingdom and the United States of America, Her Majesty’s Stationery Office, London, 1961.
“The First Time Balls” Ian R. Bartky and Steven J. Dick, Journal for the History of Astronomy Volume 12 Part 3, October, 1981. At http://psyche.usno.navy.mil/millennium/timart.html
Holyhead web site: http://www.holyhead.com/page65.html
International Meridian Conference:
http://greenwich2000.com/millennium/info/conference-finalact.htm
Régimes Horaires pour le Monde Entier Henri Le Corre, Éditions Traditionnelles, 11, quai Saint-Michel – 75005 Paris, 1987.
“Time Changes in Great Britain” David Fisher, Astrological Association, London, 1991. (What I have is a 2-page photocopy.)
Time Zones: http://sts.sunyit.edu/timetech/timezones.html
http://www.fremo.org/betrieb/timezone.htm
Uniform Time Act: http://www4.law.cornell.edu/uscode/15/260a.text.html
http://www.senate.gov/~dpc/crs/reports/ascii/98-99